「カイ二乗検定って何?」「統計を知らない初心者にも分かりやすく教えてほしい」
本記事はこういった悩むを持つあなたに向けて書いています。統計学をこれから学ぶ初心者の人にも分かりやすくまとめていますので安心してお読みください。
本記事を読めば次のことが分かります。
本記事まとめ
- カイ二乗検定とは
- カイ二乗検定の流れ
- カイ二乗値
- カイ二乗分布の値
- カイ二乗分布の値とカイ二乗値を比較して結論を出す

カイ二乗検定とは
カイ二乗検定とは、カテゴリーデータ同士の関連性を調査するときに使われる手法です。
カテゴリデータの関連性を調べる際には、主にクロス集計の結果から検定が行われることが多いです。
他にカテゴリデータ以外にも、データの母分散の検定やデータの分布の適合度にも使用されます。
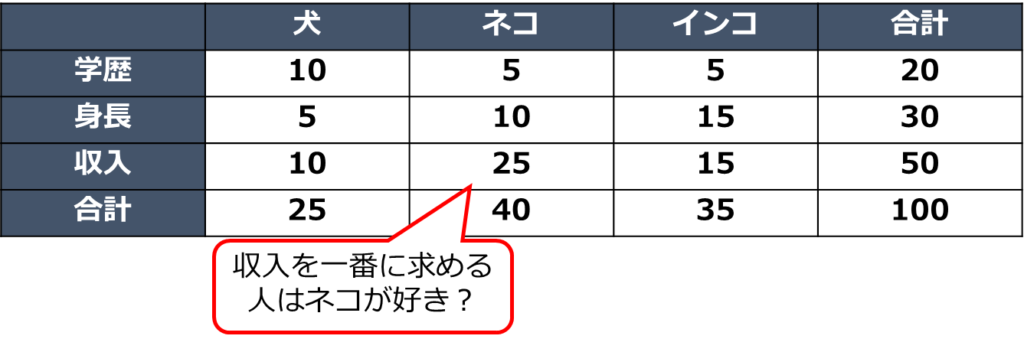
例えば、好きなペットと恋人に一番に求めるもののアンケート結果をクロス集計にまとめたものがあるとします。
この集計表を見ると、収入を一番に求める人はネコが好きな人が多そうですが、実際に関係性があるのかは分かりません。
カイ二乗検定では、この関係性を把握するのに用いることができます。
カイ二乗検定の流れ
カイ二重検定の流れについて説明していきます。
カイ二乗検定では、カイ二乗値とカイ二乗分布の値を比較して行います。
それぞれの計算の大まかな流れは次の通りです。
- 1. カイ二乗値を計算する
- 2. カイ二乗分布を求める
- 3. カイ二乗値とカイ二乗分布を比較して結論を出す
カイ二乗値とカイ二乗分布の算出方法や求め方は次の通りです。
カイ二乗値の求め方
- 帰無仮説と対立仮説を決めて結論を出す
- 有意水準で帰無仮説の採用・不採用を決める
- カテゴリデータの傾向を計算する
- カイ二乗値を計算する
カイ二乗分布の値の求め方
- 自由度を求める
- 自由度と有意水準を参考に表から見つけ出す
ここからは上記について詳しく解説していきます。
帰無仮説・対立仮説や、有意水準についてはこちらの詳しくブログで解説していますので、是非参考にしてみてください。
カイ二乗値
帰無仮説と対立仮説を用いて結論を導く

帰無仮説は否定したい仮説、対立仮説は帰無仮説の代わりとなる仮説です。
今回は好きなペットと恋人に一番に求めるものの関係性がありそうなことを結論に示したいとします。
この時、帰無仮説は「好きなペットと恋人に一番に求めるものに関係性がない」、対立仮説はその反対の「関係性がある」となります。
有意水準で帰無仮説の採用・不採用を決める

有意水準は帰無仮説を棄却する確率の基準値を定めたものです。
ここでは、有意水準を良く使用される5%に設定したとします。

計算される数値から得られた確率が5%を下回っている場合、帰無仮説を棄却することができます。
カテゴリデータの傾向を計算する
ここからは帰無仮説をもとに、検定を行っていきます。
検定ではクロス集計表から関係性とカテゴリの傾向をそれぞれ見出していきます。
関係性とカテゴリの傾向を見出す方法は次の通りです。
関係性
それぞれのペット好きな人が恋人に求めるものの傾向が全て同じでない
カテゴリデータの傾向
実際に観測された値(実測値)と傾向がない場合の値(理論値)との差
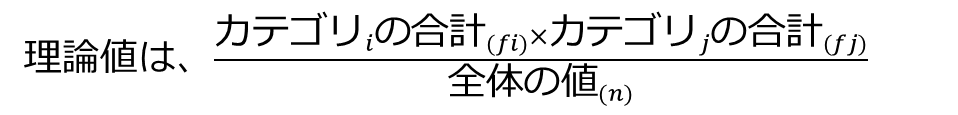
理論値は、対象となるカテゴリデータの合計値同士を掛け合わせ、全体の合計を割ったもので算出されます。
例えばデータ全体の傾向がないときに、好きなペットが犬の場合かつ学歴を求める場合の理論値は次の様に計算できます。
犬が好きかつ、学歴を求める場合
(好きなペットが犬(25)×学歴を求める(20))/全体の合計(100)=5
これを全てのデータで計算すると表は次の通りになります。

そして実測値から理論値を引いてカテゴリデータの傾向を求めていきます。
カテゴリデータの傾向は次の式で算出することができます。


赤字で表示している値がそれぞれのデータの傾向の特徴を表しています。
カイ2重値を計算する
最後に算出した値を合計します。この合計値をカイ2乗値と呼びます。
計算式は次の通りです。

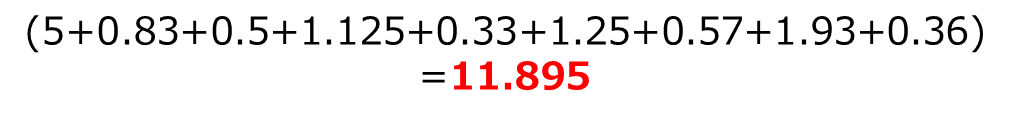
計算結果は11.895となりました。この値から、カテゴリデータの傾向があるかないかをカイ2乗分布を用いて判定していきます。
カイ二乗分布の値
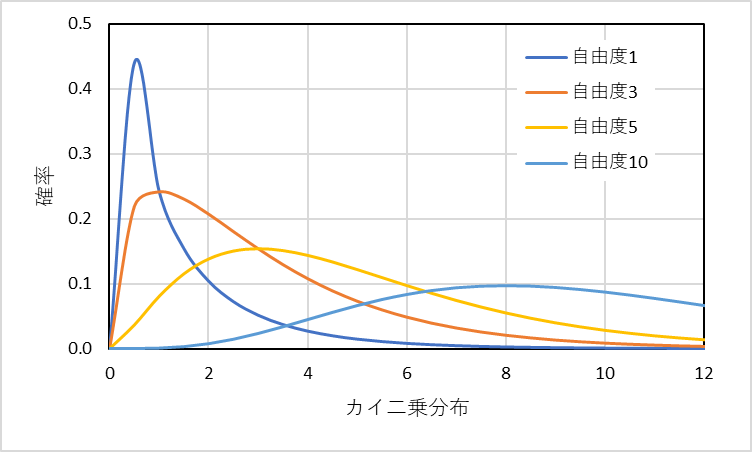
カイ二乗分布は確率分布の1種で、複数の独立した正規分布から得られます。
グラフは縦軸が確率、横軸がカイ二乗値をそれぞれ表しています。
カテゴリ数やデータ数に応じて自由度が変わり、それによってグラフの曲線も変化します。
この分布を用いてカテゴリ同士の関連性を把握することが可能です。
自由度を計算する
まずカイ二乗分布の値を求めるには、自由度と有意水準が必要になり、この値から表などを参考に見つけていきます。
自由度
自由度は『カテゴリデータの種類-1』×『カテゴリデータの種類-1』で求めることができます。
ここで検証しているデータは好きなペットが犬・ネコ・インコの3カテゴリと恋人に求めるものが学歴・身長・収入の3カテゴリでした。
そのため、自由度は(3-1)×(3-1)=4となります。
自由度と有意水準を参考に表から見つけ出す
今回、有意水準は5%に設定していたので、カイ二乗分布表でそれに該当する場所を探します。

カイ二乗分布表は縦軸に自由度、横軸に有意水準(小数点表示)を示しています。
自由度4、有意水準5%は表の中で9.49が該当し、これがカイ二乗分布の値となります。
カイ二乗分布の値とカイ二乗値を比較して結論を出す
それでは実際にカイ二乗分布の値とカイ二乗値を比較してみます。
カイ二乗分布の値は9.49でカイ二乗値は11.89でしたので、それぞれを自由度4のグラフ上に表すと下のグラフの様に示すことができます。
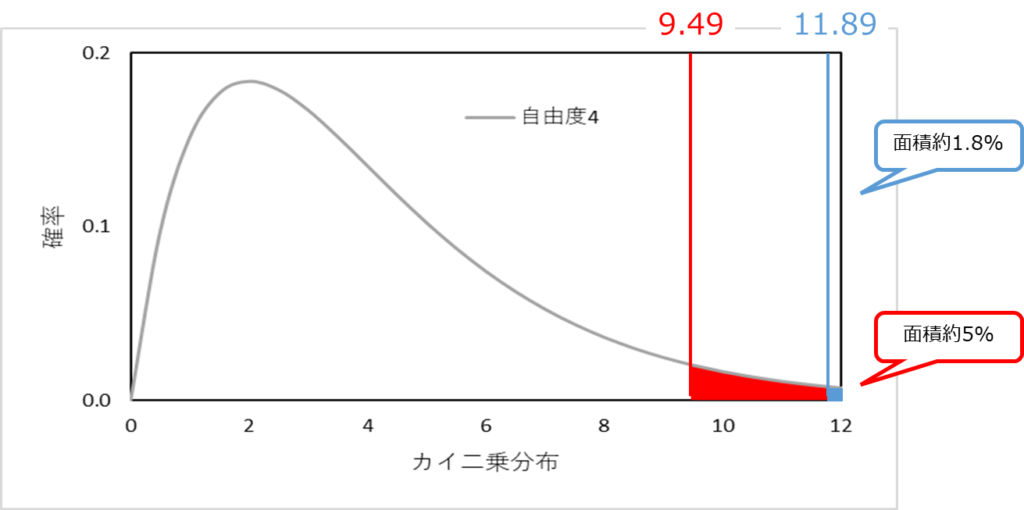
9.49と11.89はグラフ上ではそれぞれ、赤棒と青棒の位置で表示することができます。
次に9.49で表示された赤棒から右側の面積と11.89で表示された青棒から右側の面積を合計します。
面積の合計
- 赤棒から右側の面積:全体の約5%
- 青棒から右側の面積:全体の約1.8%
赤棒から右側の面積よりも青棒の右側の面積の方が小さいため、カイ二乗分布の値よりもカイ二乗値の方が確率が低いことが分かりました。
つまり、今回のアンケートで発生した傾向は偶然ではないと判断することができ、帰無仮説を棄却することができます。
「カイ二乗分布の値<カイ二乗値」のため帰無仮説を棄却

最後に好きなペットと恋人に求めるものに関係性があると判断することができました。
まとめ
いかがでしたでしょうか^^
本記事では統計学を初めて学ぶ初心者のためにカイ二乗検定について解説しました。
カイ二乗検定では、カイ二乗値とカイ二乗分布の値を比較して行います。
それぞれの計算の大まかな流れは次の通りです。
- 1. カイ二乗値を計算する
- 2. カイ二乗分布を求める
- 3. カイ二乗値とカイ二乗分布を比較して結論を出す
カイ二乗値とカイ二乗分布の算出方法や求め方は次の通りです。
カイ二乗値の求め方
- 帰無仮説と対立仮説を決めて結論を出す
- 有意水準で帰無仮説の採用・不採用を決める
- カテゴリデータの傾向を計算する
- カイ二乗値を計算する
カイ二乗分布の値の求め方
- 自由度を求める
- 自由度と有意水準を参考に表から見つけ出す
帰無仮説・対立仮説や、有意水準についてはこちらの詳しくブログで解説していますので、是非参考にしてみてください。


