【超初心者向け】相関分析について詳しく解説

「相関分析って何？」「統計を知らない初心者にも分かりやすく教えてほしい」

本記事はこういった悩むを持つあなたに向けて書いています。統計学をこれから学ぶ初心者の人にも分かりやすくまとめていますので安心してお読みください。

そこで本記事では統計学を初めて学ぶ初心者のために相関分析について解説します。

本記事を読めば次のことが分かります。

それでは上記について詳しく解説していきます。

相関分析とは

相関分析とは、2つデータの関係性を関係性を理解するの手法として使われます。

相関分析には比較したい2つのデータが「どの程度関係しているのか」を明らかにし、データ同士の特徴を把握しやすいといった特徴があります。

それでは次に相関分析をするために重要な相関について解説してきます。

相関について

それではまず、相関について説明していきます。

相関とは2つの量的データの直線的な関係性を指します。

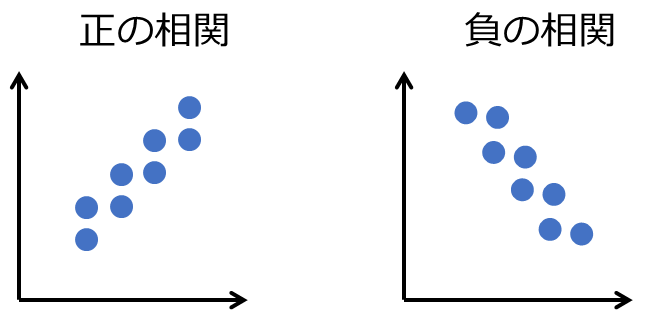
相関には正の相関と負の相関があり、その度合いを相関係数という値で示すことができます。

正の相関とはあるデータが増加すると、もう片方も増加する関係を言います。一方で、負の相関はあるデータが増加するともう片方は減少します。

相関係数と混合しやすいものとして因果関係がありますので、次は因果関係についてご説明いたします。

因果関係について

因果関係とは原因とそれによって生ずる結果の関係を表しています。

例えば、収入と運動能力に負の相関がある場合を考えてみます。

このグラフでは収入が高いほど、運動能力が低い関係性を示しています。

年齢が上がるにつれて会社内での役職が上がり収入が増える一方で、加齢による運動能力の衰えなどが考えられます。

一方で相関関係のように「運動能力が低いため、収入が少ない」とは言えません。

相関係数について

ここでは相関係数についてご説明いたします。

相関係数とは、2つのデータ量の相関関係を数値化したもののことを言います。

相関関係についてまとめると次の通りです。

散布図は正の相関が強いとは右肩上がりに、負の相関が強いと左肩上がりに並びます。

正の相関が近いと相関係数は1、負の相関が近いと相関係数は-1にそれぞれ近づいていきます。

一方で、相関係数が0に近い場合、散布図はバラバラにデータが散らばっており、2つのデータに相関はないと判断できます。

相関係数は次の式によって求めることができます。

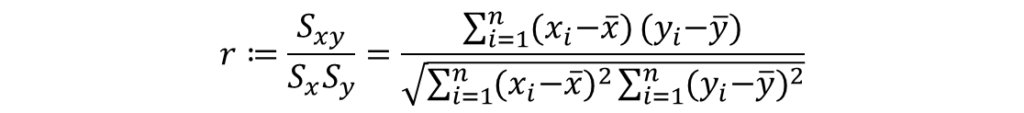
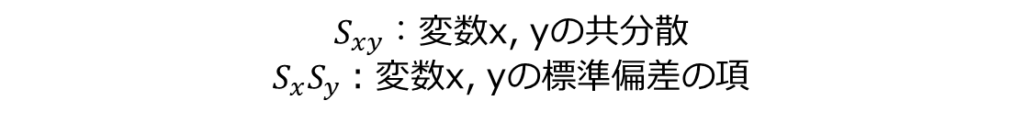
式中の分子は2つのデータの共分散、分母は標準偏差の項をそれぞれ示しています。

共分散のみでも相関係数のように、2つのデータの増減関係を示すことはできます。

分子の共分散を分母の標準偏差の項で割ることで単位を揃え、他の項目と比較しやすいようになっています。

相関係数を閾値として使うことでデータ間の相関度合いを把握したりします。

まとめ

いかがでしたでしょうか^^

本記事では統計学を初めて学ぶ初心者のために相関分析について解説しました。

相関分析とは、2つデータの関係性を関係性を理解するの手法として使われます。

相関係数は2つのデータの共分散と標準偏差から算出することができ、まとめると次の通りです。

帰無仮説・対立仮説や、有意水準についてはこちらの詳しくブログで解説していますので、是非参考にしてみてください。