「t検定って何?」「統計を知らない初心者にも分かりやすく教えてほしい」
本記事はこういった悩むを持つあなたに向けて書いています。統計学をこれから学ぶ初心者の人にも分かりやすくまとめていますので安心してお読みください。
本記事を読めば次のことが分かります。
本記事まとめ
- t検定の概要
- 1標本検定について
- 2標本検定(対応あり・なし)について
それでは上記について詳しく解説していきます。
t検定の概要
t検定とは
t検定とは少ないサンプル数でも仮説の正しさを統計的な方法を利用して確認できる方法のことを言います。
例えば、あなたがA店のスタッフだったとします。
A店の売り上げが他店と比較してあまりよくなかったので、その原因を探るためにアンケートを行いました。
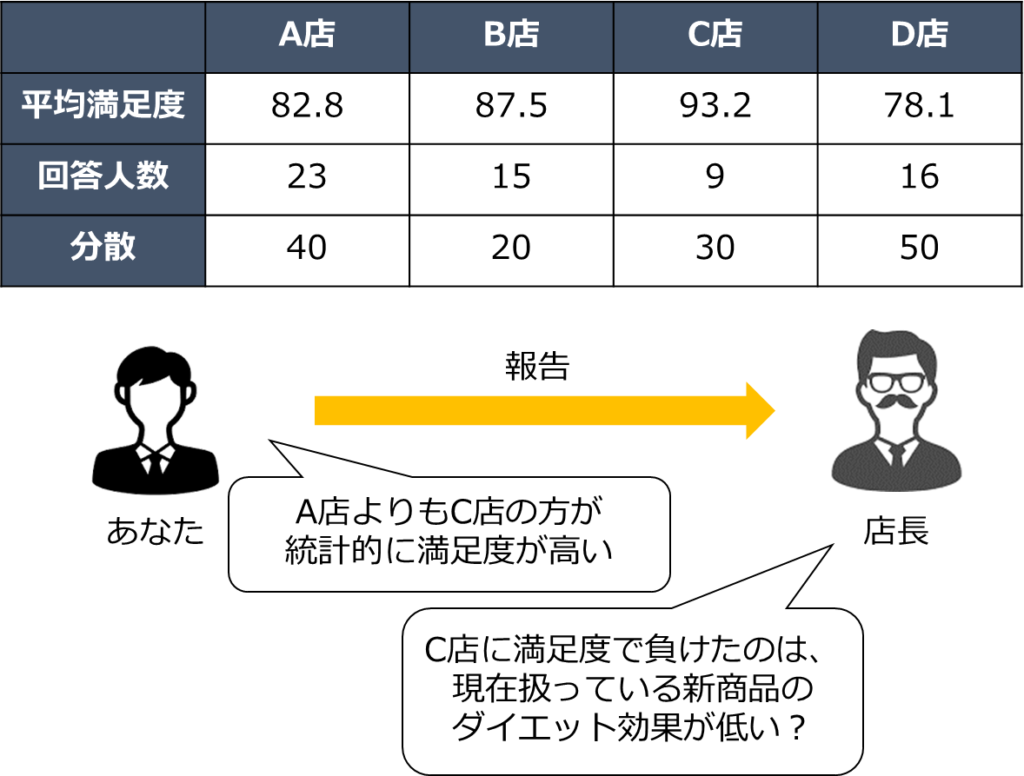
あなたは全体的な満足度を調査した結果、次の表に示す結果が得られました。

このアンケート結果からA店はB店やC店と比較して平均満足度が低いことが分かります。
しかしながら、回答人数は店舗によってバラつきがあるため、この平均満足度をそのまま信じてよいか分かりません。
この平均満足度の違いが本当にあるのかを統計的に確認する方法が標本検定です。
t検定の流れについて
t検定の大まかな流れは次の通りです。
t検定の流れ
- 帰無仮説を対立仮説を決める
- 対立仮説から仮説を考える
- 有意水準を決め、棄却域を計算
- 数式に従ってt値を計算する
- 棄却域から帰無仮説を棄却するかを決める
基本的にt検定で扱う数値は平均や分散・確率などどのような差でも同じ流れで検定を行います。
それでは上記について詳しく解説していきます。
- 1. 帰無仮説と対立仮説を決める
- 2. 対立仮説から仮説を考える
- 3. 有意水準を決め、棄却息を計算
帰無仮説・対立仮説や、有意水準についてはこちらの詳しくブログで解説していますので、是非参考にしてみてください。
仮説について
仮説には両側対立仮説と片側対立仮説の2種類があり、これは対立仮説に応じて使用するものが変わります。
仮説の使い分けは次の通りです。
| 条件 | |
| 両側対立仮説 | 調査した値が他と比べて違うかを知りたいとき |
| 片側対立仮説 | 調査した値が他と比べて上がったか、下がったのかを知りたいとき |
両側対立仮説は店ごとの平均満足度の調査結果に差があるのか、片側対立仮説では、A店の平均満足度よちB店やC店の満足度が本当に高いのかを調べたいときに使用します。
先程のアンケートの例だと次のようにイメージできます。
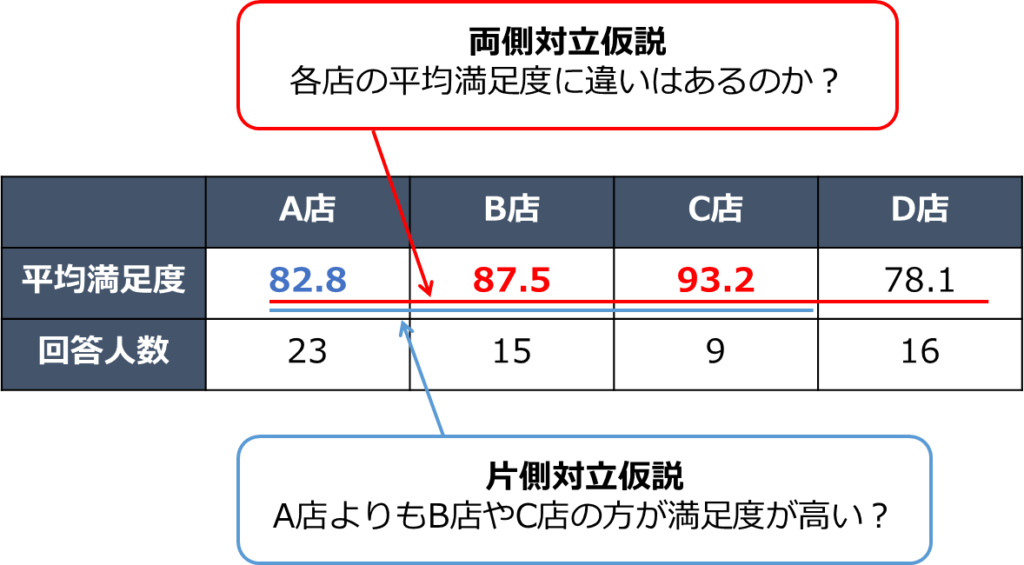
それでは次からは1標本検定と2標本検定について事例を交えながら解説していきます。
1標本検定
1標本検定とは、母集団が1つのものに対して行う検定のことです。
この検定は立てた仮説が本当に正しいのかを調べる時に使用できます。
あなたが先程のアンケート結果を店長に報告したとします。
すると店長は「別のアンケートではA店は90くらいだったので、今回の結果は偶然低く出ていないか?」と少し疑問を持たれました。
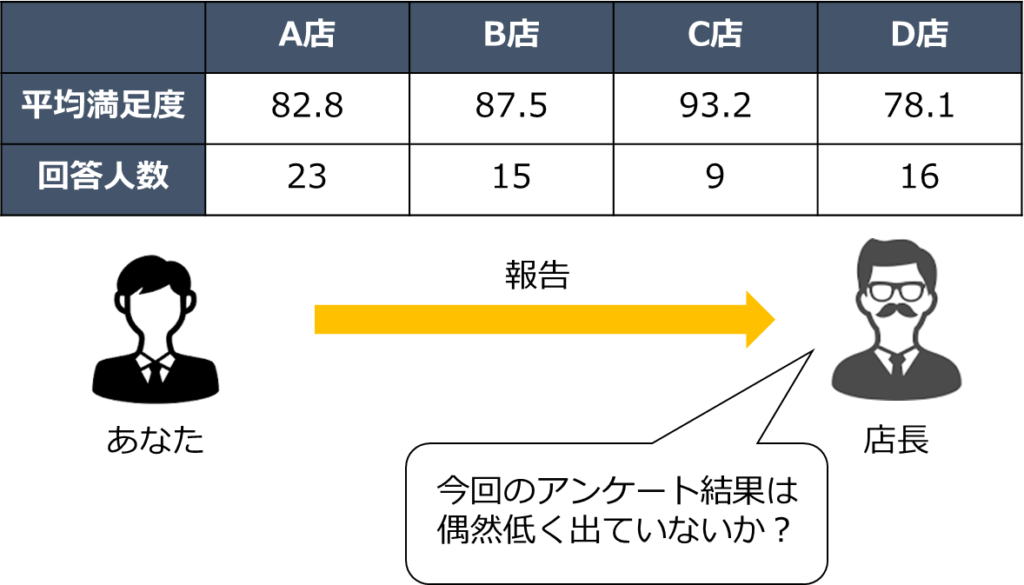
この店長のように、実際のアンケート調査結果と違うかを検証するときに1標本問題を適用することができます。
それではここからは、t検定の流れに沿って1本標本検定を進めていきます。
帰無仮説を対立仮説を決める
それではまず、帰無仮説と対立仮説を決めていきます。
この事例の場合、店長は「別のアンケートではA店の評価が90点くらいだったので、今回のアンケートは偶然低かった」と疑問を抱いています。

つまり、仮説(店長の平均90点)と結果(平均82.8点)には差がないと主張しているので、帰無仮説の母平均は90と示すことができます。
一方で、対立仮説は帰無仮説の逆を示せればよいので、仮説(店長の平均90点)と結果(平均82.8点)には差があり、母平均は90ではないとなります。
まとめると次の通りです。
帰無仮説と対立仮説
帰無仮説
仮説(店長の平均90)と結果(平均82.8)の差がない
母平均:μ=90
対立仮説
仮説(店長の平均90)と結果(平均82.8)の差がある
母平均:μ≠90
対立仮説から仮説を決める
次に対立仮説から仮説を決めていきます。
今回の問題では、対立仮説から仮説(店長の平均90)と結果(平均82.8)の差があることを示したいと考えています。
そのため、仮説の種類は両側対立仮説を選びます。
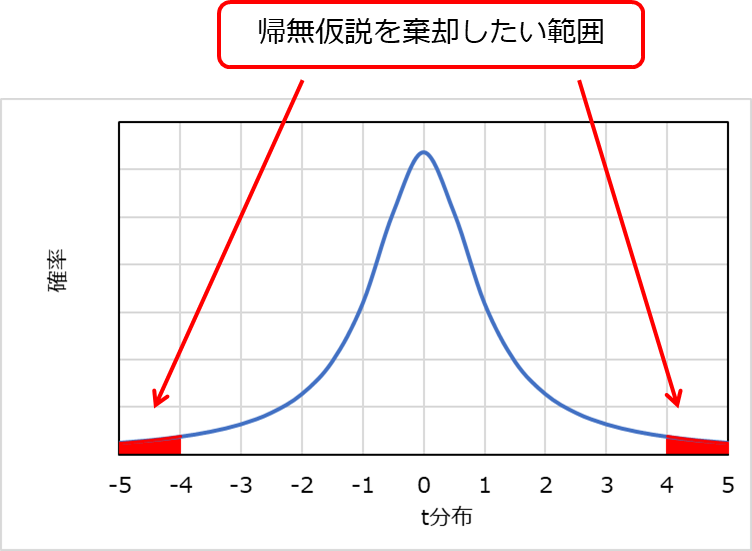
両側対立仮説ではt分布が示す範囲のうち、起こりうる確率が低いときと、高いときで帰無仮説を棄却したい範囲を設定します。
有意水準を決め、棄却域を計算する
それでは、有意水準を決め、棄却域を計算していきます。
この棄却域はt分布や標準正規分布などから決めることができます。
有意水準の確率はここではよく使われる5%に設定して棄却域を計算していきます。
今回のアンケートでは母分散が未知なので、自由度と有意水準を参考に棄却域を求める必要があります。
ここでのA店についてのアンケート回答人数は23だったので、自由度は22となります。
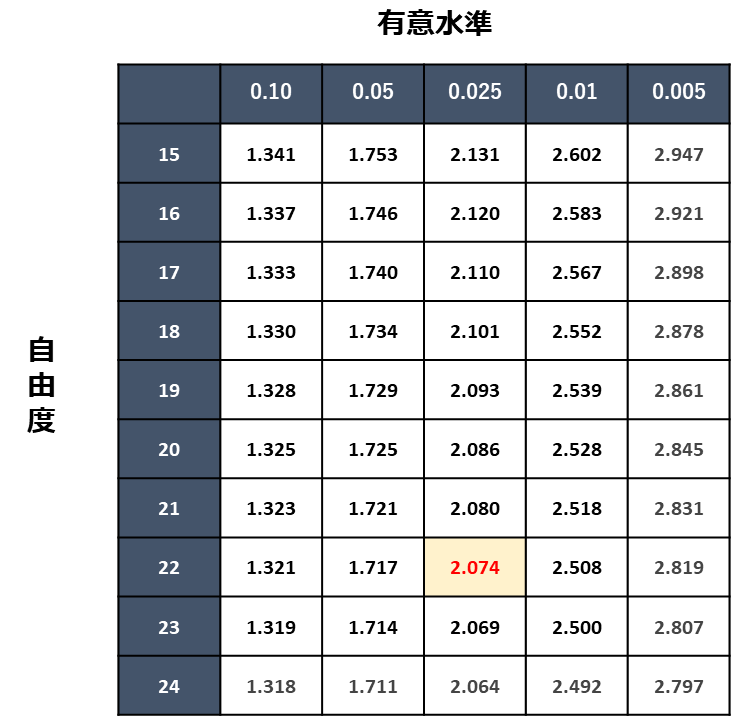
有意水準表より、自由度22、有意水準の確率5%に該当する値は2.074です。
両側対立仮説の場合、分布の両側の確率を合わせて有意水準の確率にしているため、有意水準の確率÷2がt値を算出する際に使われます。
両側検定なので、2.074よりも大きいもしくは、小さい範囲を棄却域と呼びます。
ここでの棄却域を求める方法はこちらのブログで解説していますので、是非参考にしてみてください。
数式に従ってt値を計算する
次は数式に従ってt値を計算していきます。
今回のアンケートの様に母分散が未知の場合は、t検定の数式から求めていきます。
t検定の数式
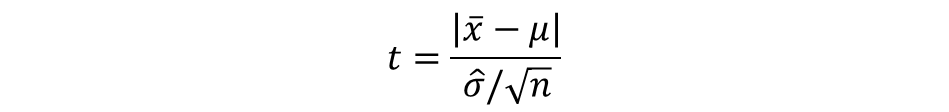

上の数式から算出される値をt値と呼びます。
母分散が既知の場合はz検定となり、不偏分散ではなく分散を使用します。
ここの数式は母分散や標本の数などの調査の条件に応じて計算が変わるので注意が必要
こちらの数値を用いて計算していくと次のように求めることができます。


棄却域から帰無仮説を棄却するかを決める
それでは最後に棄却域から帰無仮説を棄却するかを決めます。
t分布からの棄却域は2.074、t値の計算結果は4.94であり、次のグラフの様に示すことができます。
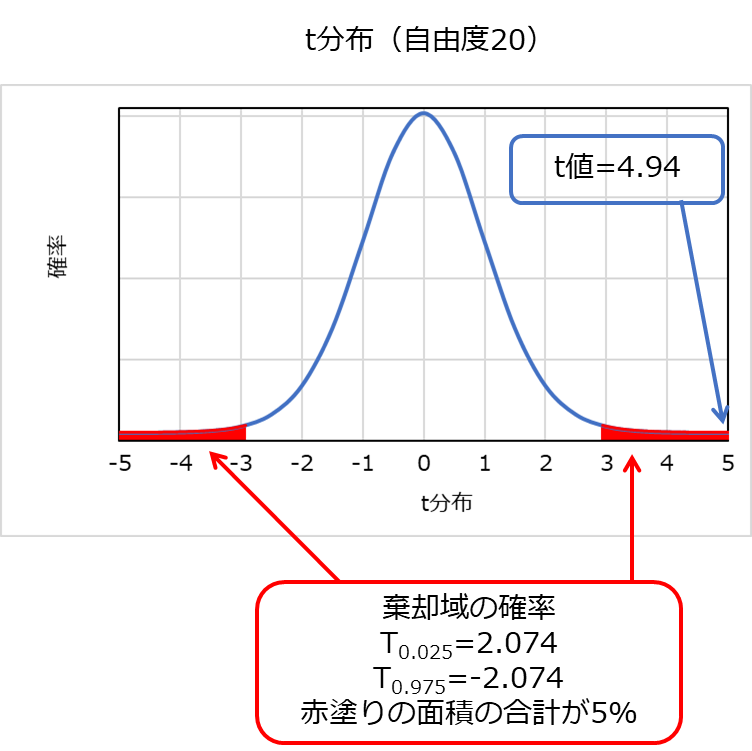
この結果から棄却域の2.074よりもt値の4.94の方が値が大きいため、帰無仮説を棄却することができます。
棄却域とt値の比較
有意水準5%のt値(棄却域):2.074
t検定の計算結果(t値):4.94
棄却域<t値なので、帰無仮説を棄却することができる
すなわち、店長の仮説であったμ=90を棄却し、対立仮説であるμ≠90を採択したため、アンケート結果が正しい可能性が高いことが分かりました。
2標本検定
それでは次に2標本検定について説明していきます。
2標本検定とは2つの標本を使用して行う検定のことであり、調査結果から得られた違いを統計的に比較することができます。
2標本検定には『対応なし』と『対応あり』の2種類があります。
対応あり・なしの違いについて
- 対応なし
異なる標本から得られた数値の違いを検定する - 対応あり
同じ標本から得られた数値の違いを検定する
それではそれぞれの違いにについて詳しく解説していきます。
対応なし
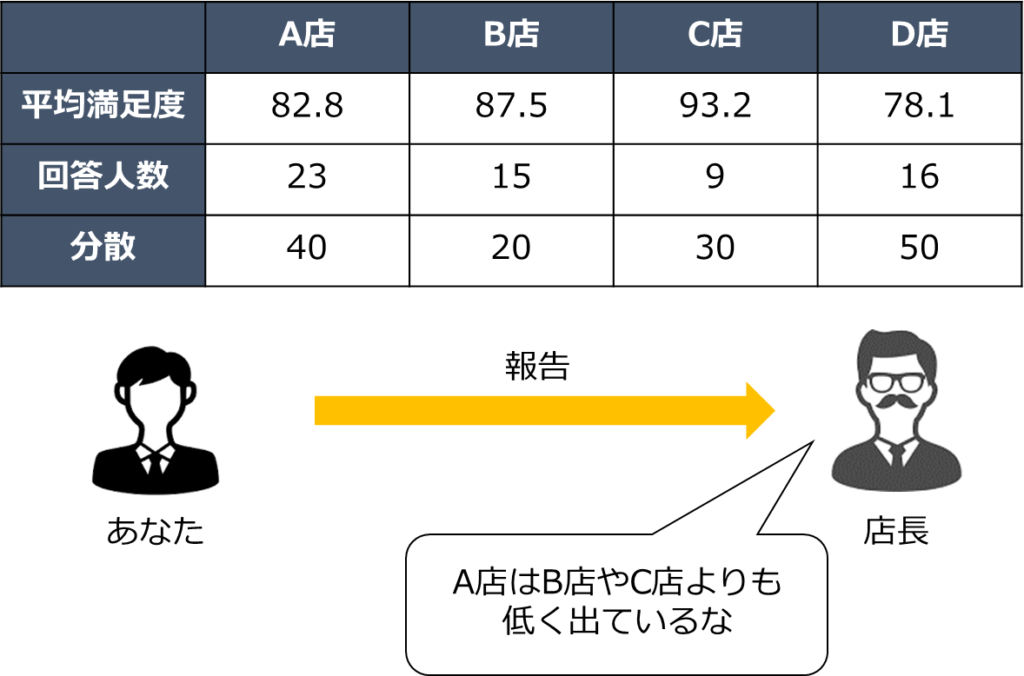
対応なしの場合は、例えば、1人1回しか回答することができないアンケート結果から、店舗ごとの満足度の違いを比較するときに使用することができます。
この場合、店舗を利用している人は違うので異なる標本と言えます。
対応あり
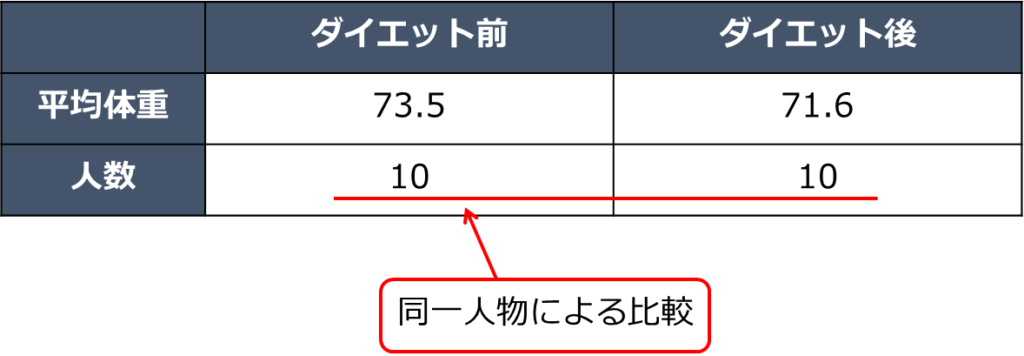
対応ありの場合は、例えば、10人の一般人にダイエットをしてもらい、ダイエット前後でどのくらい体重が変わったかを比較するときに使用できます。
これらを踏まえて『対応なし』と『対応あり』の2標本検定を解説していきます。
2標本検定(対応なし)
それでは、2標本検定の対応なしを解説していきたいと思います。
さきほどのアンケートを報告したところ、店長から次のようなコメントが来たとします。
店長『C店にはこれまで満足度で負けていなかったが、数値的にはC店は高く出ている。本当にC店よりもA店が低いのか統計的に確かめてほしい。』
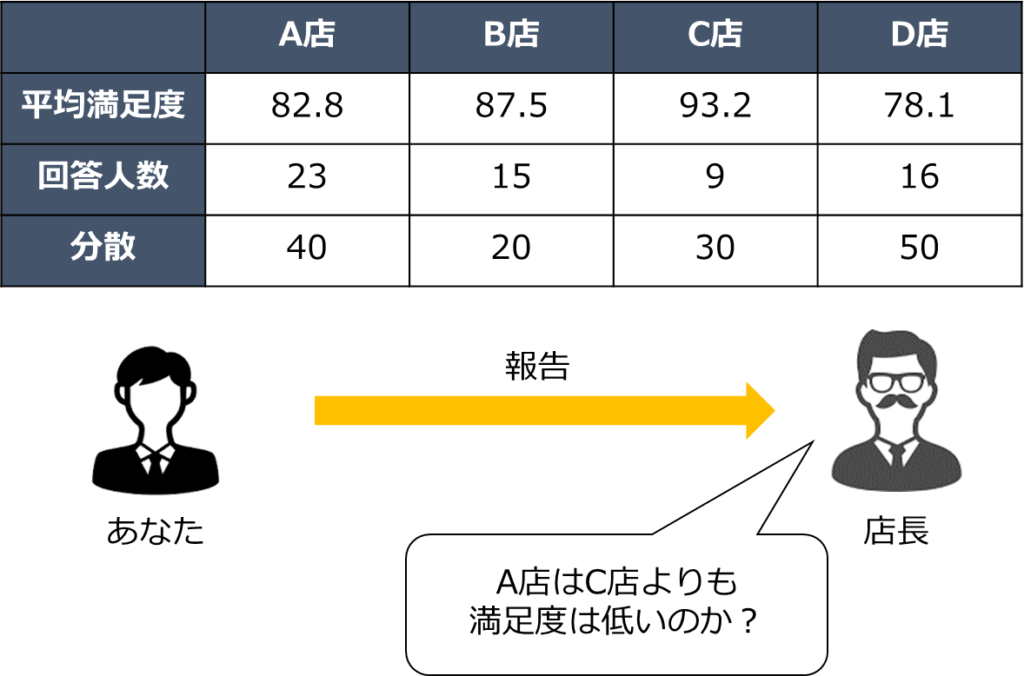
このような他店との何かを比較を行いたい場合は、対応のない2標本検定で進めることができます。
それではここからは、t検定の流れに沿って2本標本検定(対応なし)を進めていきます。
1標本問題も2標本問題も仮説検定を行う場合、t検定の流れに沿って解き進めていきます。
帰無仮説と対立仮説を決める
それではまず、帰無仮説と対立仮説を決めていきます。
この事例の場合、店長は「C店にはこれまで満足度で負けていなかったが、数値的にはC店は高く出ている。本当にC店よりもA店が低いのか」と疑問を抱いています。

つまり、帰無仮説はA店の平均満足度μAとC店の平均満足度μCには差がなく、(μA=μC)と表すことができます。
一方で、対立仮説はC店の方が平均満足度が高いことが気になっていましたので、A店よりもC店の方が平均満足度は大きく、(μA<μC)と表すことができます。
まとめると次の通りです。
帰無仮説と対立仮説
帰無仮説
A店の平均満足度μAとC店の平均満足度μCには差がない
μA=μC
対立仮説
A店よりもC店の方が平均満足度は大きい
μA<μC
対立仮説から仮説を考える
次に仮説を考えていきます。
1標本検定の事例では値が違うかを調べましたが、今回の事例ではC店の平均満足度μCがA店の平均満足度μAよりも大きいか比較を行いたいと考えます。
そのため、仮説の種類は片側対立仮説を選びます。
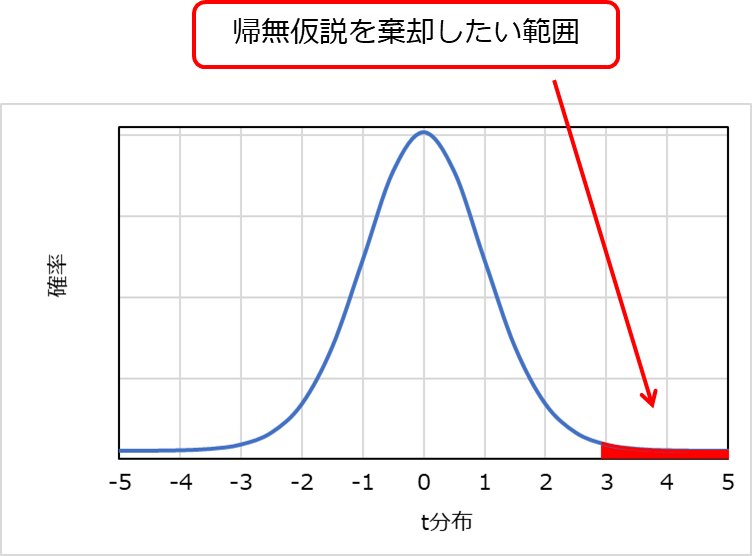
有意水準を決め、棄却域を計算する
次に有意水準を決め、棄却域を計算していきます。
この棄却域はt分布や標準正規分布などから決めることができます。
有意水準の確率はここではよく使われる5%に設定して棄却域を計算していきます。
今回のアンケートでは2標本ともに母分散が未知ですが、お互いに等しいと仮定します。
母分散が未知でお互いの母分散が等しいときにt値を求める場合、自由度の計算は(Aのサンプル数-1)+(Bのサンプル数-1)で表されます。
2標本検定の事例では母分数が既知か道によって自由度の計算が変わります。
ここでのA店のアンケート回答人数は23、C店のアンケート回答人数は9だったので、自由度は(23-1)+(9-1)=30であることが分かりました。
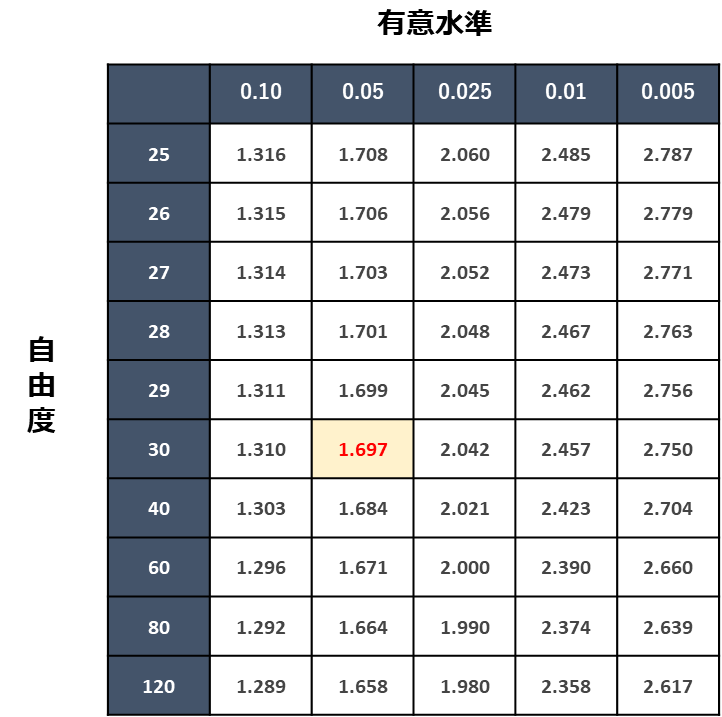
有意水準表より、自由度30、有意水準の確率5%に該当する値は1.697です。
自由度30以上の場合、補間を行う、計算ソフトを利用する、便宜的に1番近い値を選択するなどの方法があります。
ここでの棄却域を求める方法はこちらのブログで解説していますので、是非参考にしてみてください。
数式に従ってt値を計算する
次は数式に従ってt値を計算していきます。
今回のアンケートの様に母分散が未知の場合は、t検定の数式から求めていきます。
t検定の数式(2標本の分散が等しいとき)
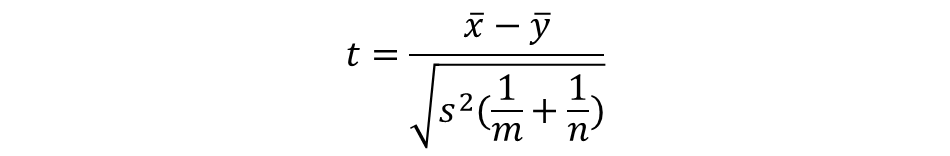

サンプル数が多ければ、母分散既知でもz検定で進めていきます。
プールした分散は次の数式で表されます。
プールした分散の数式
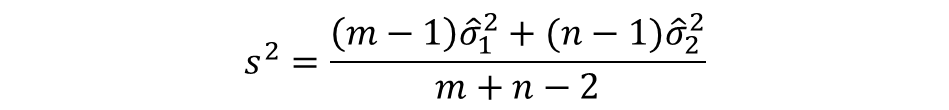

それでは、プールした分散を求めた後、t値を算出していきます。
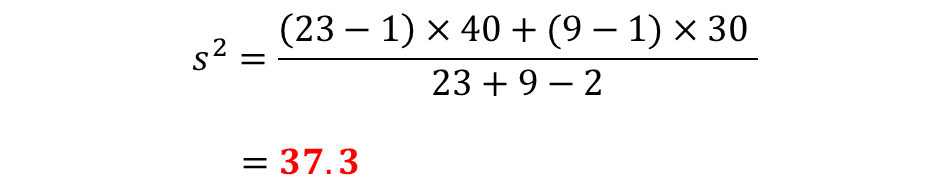
プールした分散の値からt値を求めていきます。
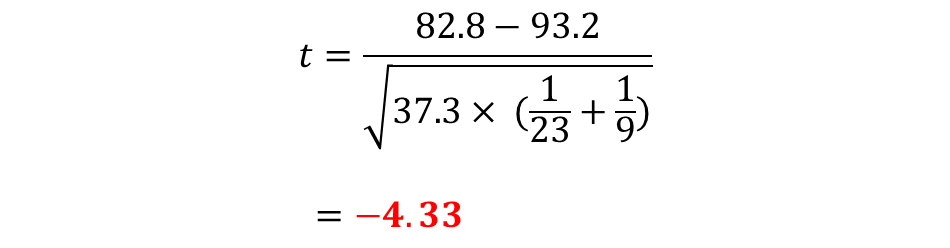
棄却域から帰無仮説を棄却するかを決める
それでは最後に棄却域から帰無仮説を棄却するかを決めます。
t分布からの棄却域は1.697、t値の計算結果は-4.33であり(|t値|=4.33)、次のグラフの様に示すことができます。
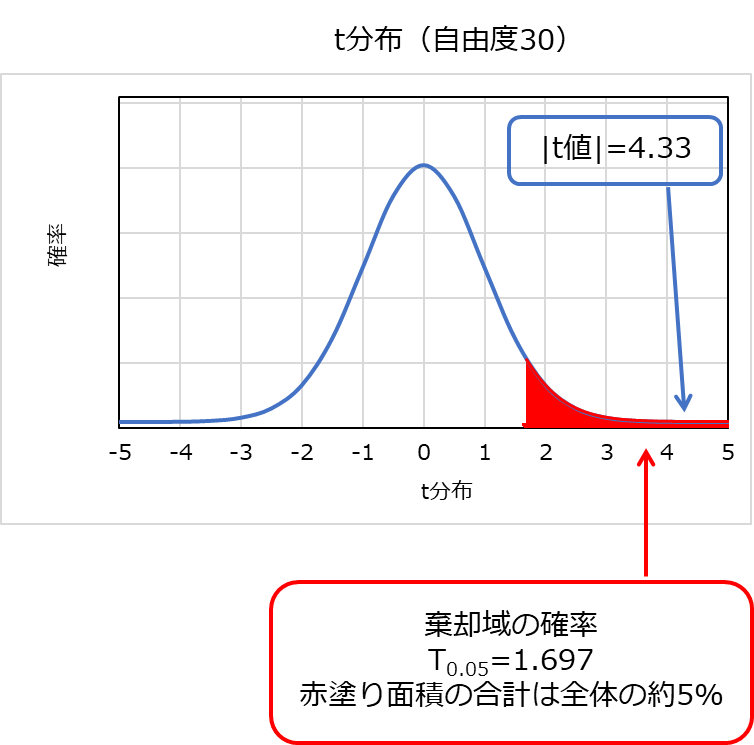
この結果から棄却域の1.697よりも|t値|の4の方が値が大きいため、帰無仮説を棄却することができます。
棄却域とt値の比較
有意水準5%のt値(棄却域):1.697
t検定の計算結果(|t値|):4.33
棄却域<|t値|なので、帰無仮説を棄却することができる
すなわち、A店よりもC店の方が満足度が高いことが統計的に求めることができました。
2標本検定(対応あり)
続いて2標本検定(対応あり)について解説していきたいと思います。
先程の対応のない2標本検定の結果、A店よりもC店の方が満足度が高いことを統計的に確認しました。
その後、店長から次のようなコメントが来たとします。
店長『C店に平均満足度で負けたのは、現在A店で扱っている新商品のダイエット効果が低いことが原因かもしれない』
そこであなたはA店の新商品のダイエット効果に対する満足度のアンケート調査を行うことにしました。
その結果次のようなことが分かりました。

このアンケート結果では新旧商品を同一顧客に回答してもらっているため、2標本で得られたサンプルが同じであり、対応のある2標本検定で進めることができます。
それではここからは、t検定の流れに沿って2本標本検定(対応あり)を進めていきます。
帰無仮説と対立仮説を決める
それではまず、帰無仮説と対立仮説を決めていきます。
この事例の場合、店長は『C店に平均満足度で負けたのは、現在A店で扱っている新商品のダイエット効果が低いことが原因かもしれない』と疑問を抱いています。

つまり、帰無仮説はA店の旧商品の満足度xiと新商品の満足度yiの差の平均μが0であり、(μ=0)と表すことができます。
一方で、対立仮説はA店の旧商品の満足度xiと新商品の満足度yiの差の平均μが0以上であり、(μ>0)と表すことができます。
まとめると次の通りです。
帰無仮説と対立仮説
帰無仮説
A店の旧商品の満足度xiと新商品の満足度yiの差の平均μが0
μ=0
対立仮説
A店の旧商品の満足度xiと新商品の満足度yiの差の平均μが0以上
μA>0
対立仮説から仮説を考える
次に仮説を考えていきます。
今回の事例ではA店の旧商品の満足度の方が新商品の満足度よりも大きいかの比較を行いたいと考えます。
そのため、仮説の種類は片側対立仮説を選びます。

有意水準を決め、棄却域を計算する
それでは、有意水準を決め、棄却域を計算していきます。
この棄却域はt分布や標準正規分布などから決めることができます。
有意水準の確率はここではよく使われる5%に設定して棄却域を計算していきます。
今回のアンケートでは2標本ともに母分散が未知ですが、お互いに等しい関係なので、自由度は(5-1)=4であることが分かりました。
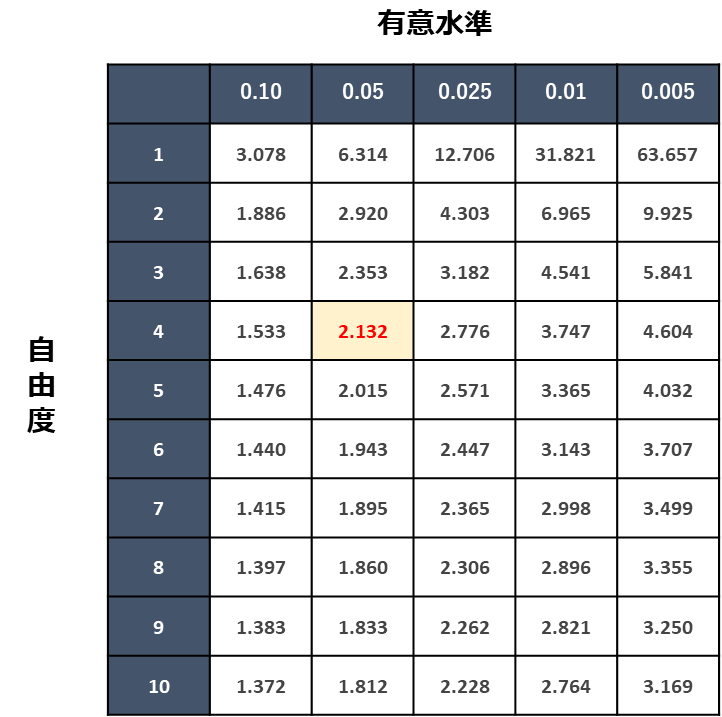
有意水準表より、自由度4、有意水準の確率5%に該当する値は2.132です。
ここでの棄却域を求める方法はこちらのブログで解説していますので、是非参考にしてみてください。
数式に従ってt値を計算する
次は数式に従ってt値を計算していきます。
今回のアンケートの様に母分散が未知の場合は、t検定の数式から求めていきます。
t検定の数式(2標本の分散が等しいとき)
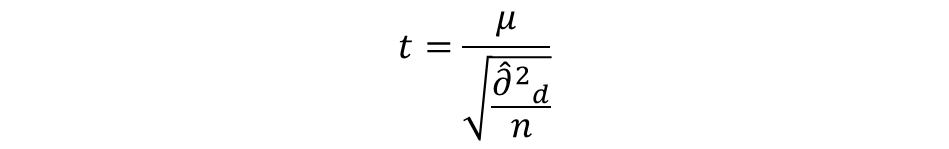

対応ある標本の差の不偏分散は次の式で求めることができます。
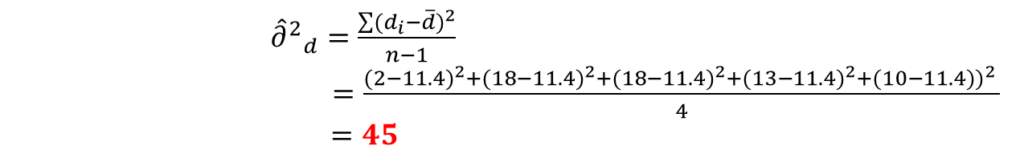

よって、ここからt値は次のように算出することができます。


棄却域から帰無仮説を棄却するかを決める
それでは最後に棄却域から帰無仮説を棄却するかを決めます。
t分布からの棄却域は2.132、t値の計算結果は3.8であることから、次のグラフの様に示すことができます。
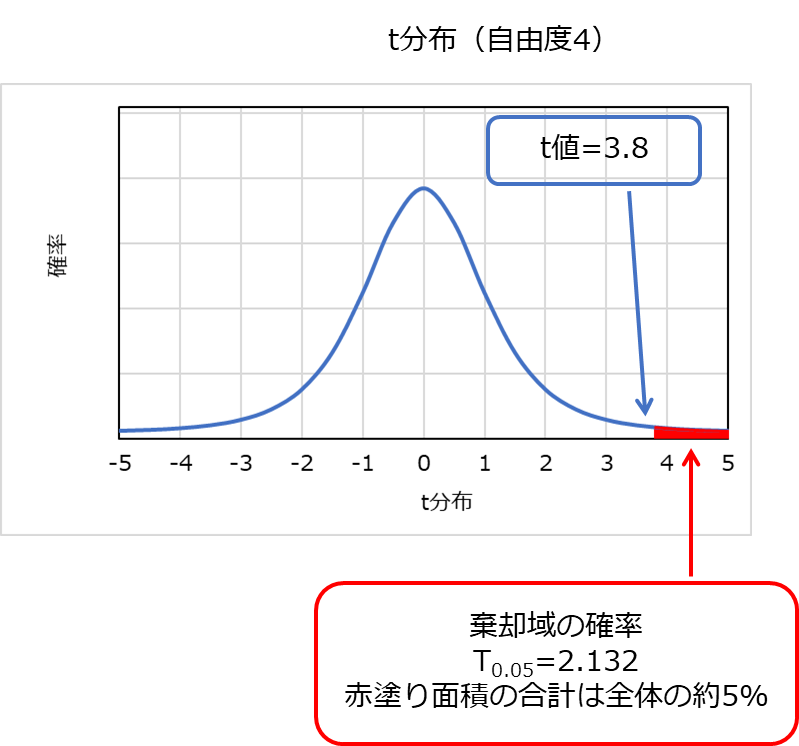
この結果から棄却域の2.132よりもt値の3.8の方が値が大きいため、帰無仮説を棄却することができます。
棄却域とt値の比較
有意水準5%のt値(棄却域):2.132
t検定の計算結果(|t値|):3.8
棄却域<t値なので、帰無仮説を棄却することができる
すなわち、A店の新商品よりも旧商品の方が満足度が高いことを統計的に求めることができました。
まとめ
いかがでしたでしょうか^^
記事では統計学を初めて学ぶ初心者のためにt検定について解説しました。
本記事をまとめると次の通りです。
本記事まとめ
- t検定の概要
- 1標本検定について
- 2標本検定(対応あり・なし)について
こちらのブログでは仮説検定や、カイ二乗検定についても詳しく解説しているので是非参考にしてください。


